 |
|||||||
Attention : cette rubrique comporte plusieurs pages ; fin de page pour la suite .... Exemple introductif : étude d'un plaque percée On considère une plaque mince (épaisseur h) circulaire, de rayon intérieur b et de rayon extéreur a. Le matériau est homogène, isotrope et on considère un comportement élastique linéaire. Les liaisons cinématiques imposées sont celles d'un appui sur le bord extérieur. On note P un chargement de cisaillement dans la direction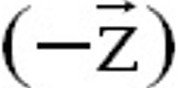 
sur le bord intérieur r = b (cf. figure 1 suivante). 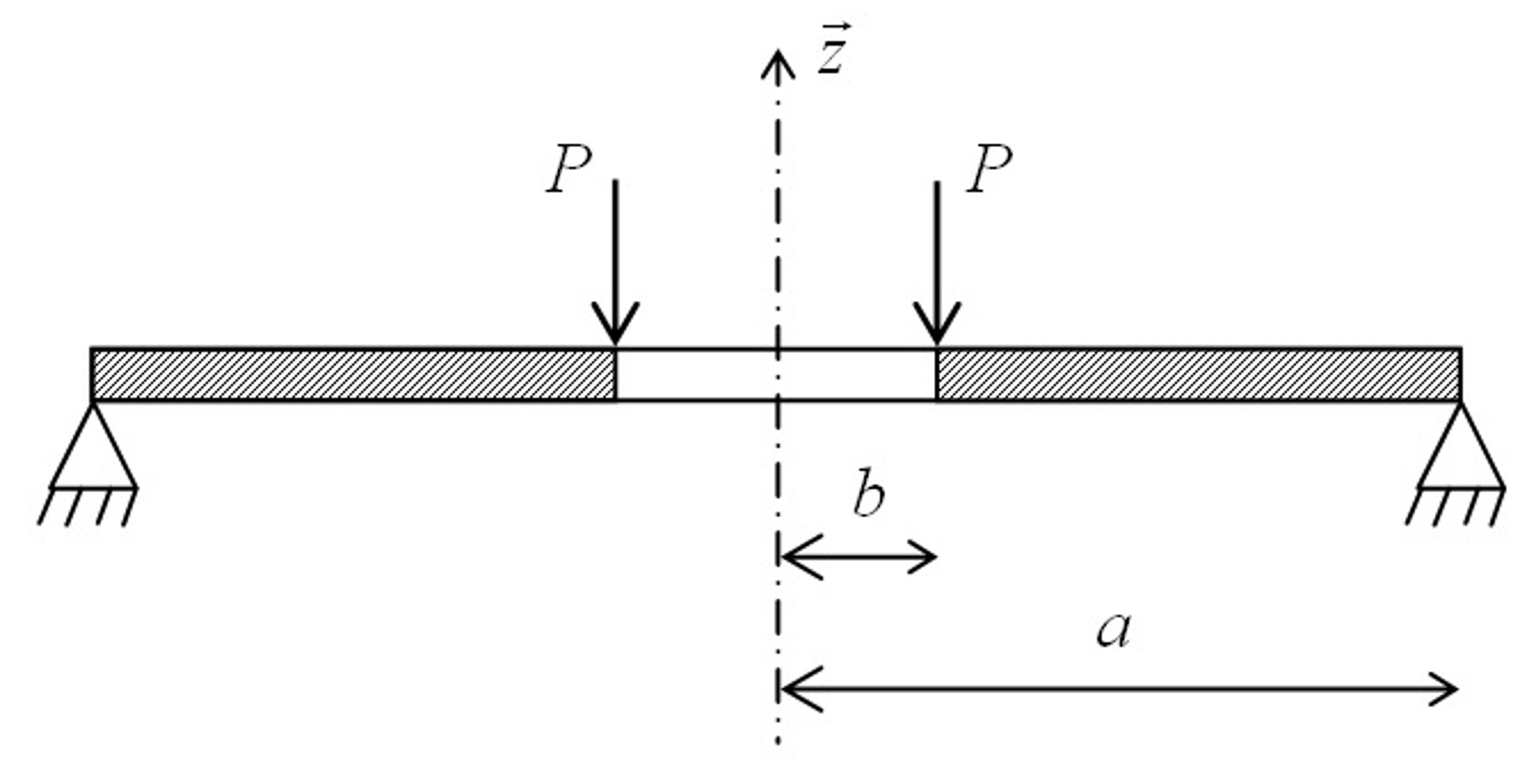Figure 1. Présentation du problème On peut montrer, en théorie des plaques (c'est à dire sous certaines hypothèses), que le déplacement suivant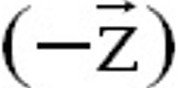
est donné par l'équation suivante : 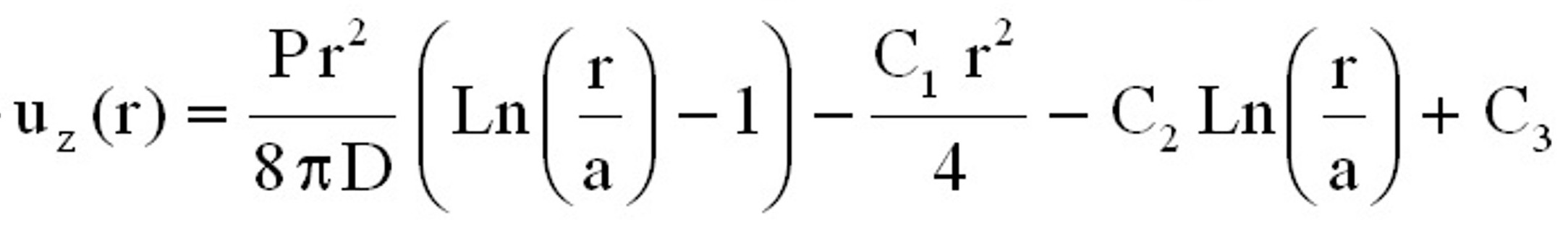avec 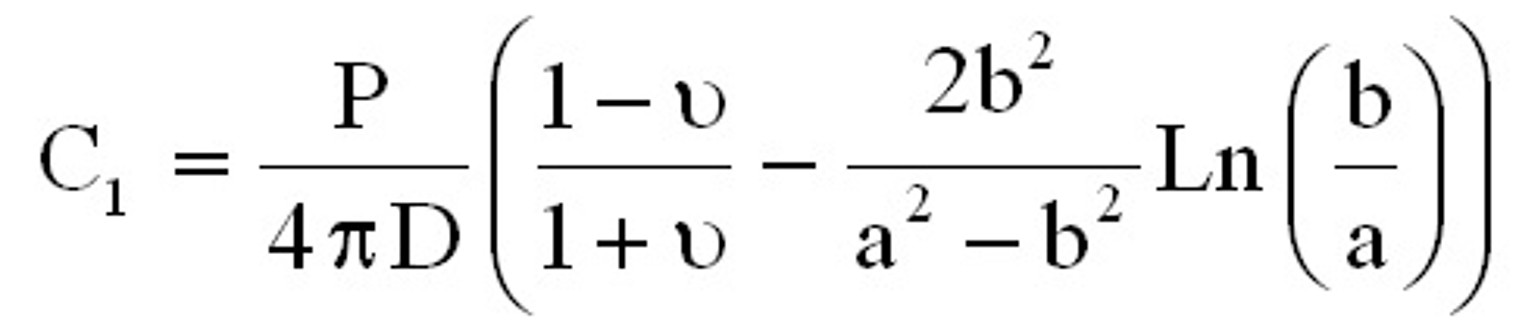 ,  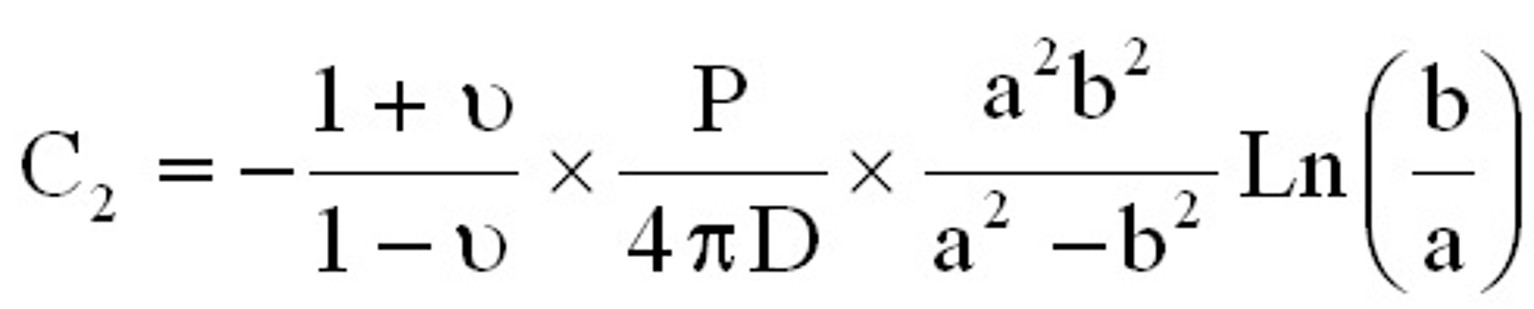et 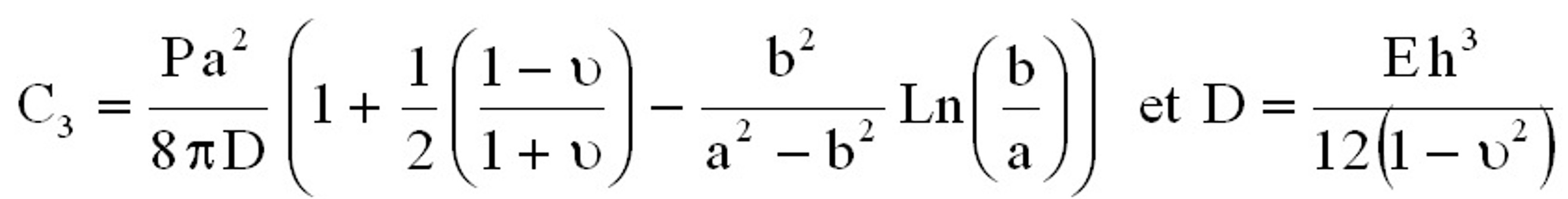 On se propose donc de comparer ce résultat issu de la théorie des plaques avec la simulation éléments finis et le logiciel CosmosWorks. Pour cette étude, les dimensions de la plaque sont les suivantes : a = 50 mm, b = 10 mm, h = 1 mm, P = 100 N. Il faut, avant le calcul éléments finis, dessiner la pièce dans SolidWorks. Pour faciliter la mise en place des conditions aux limites, on rajoutera un axe de référence, voir figure 2. 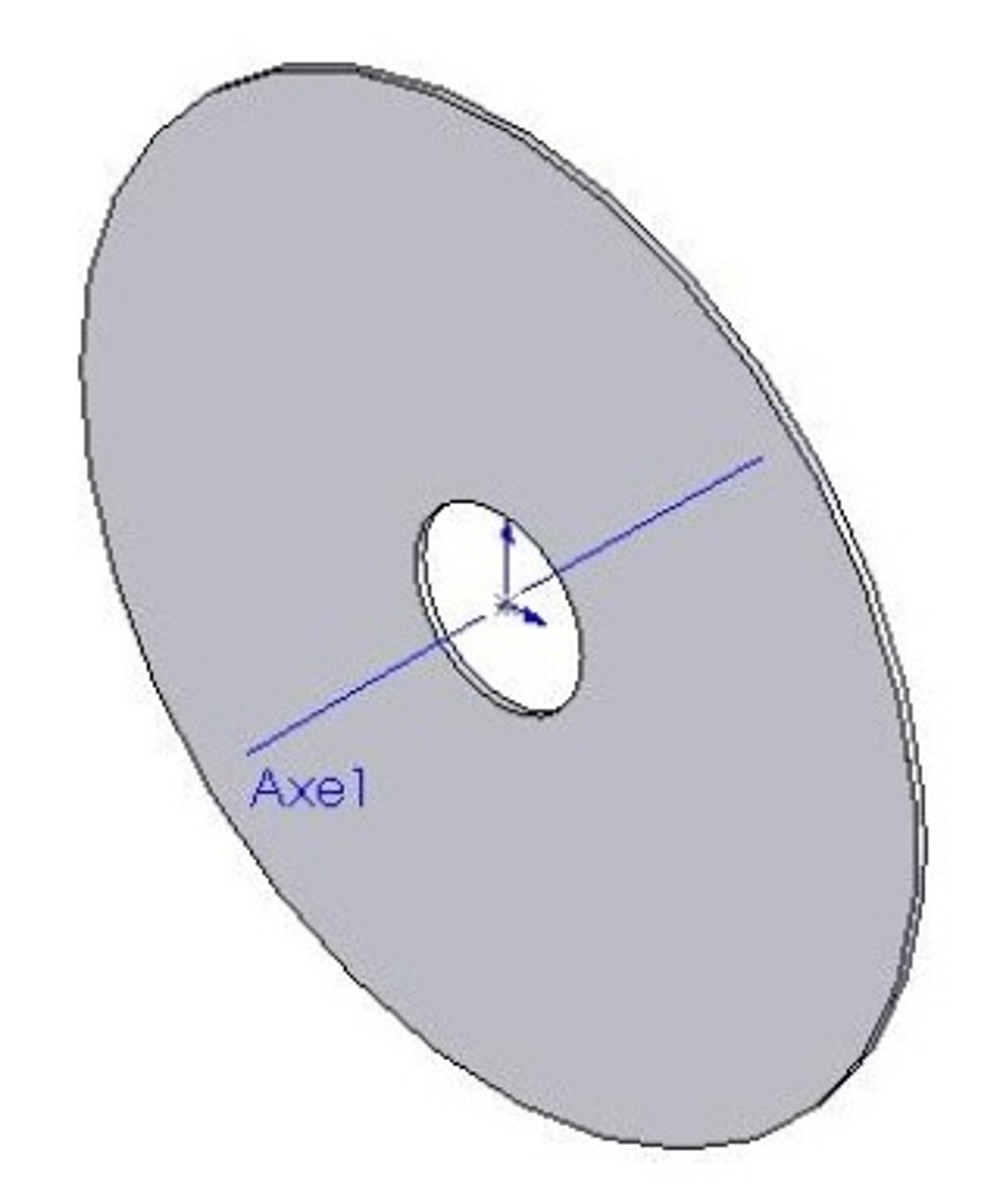 Figure 2. Dessin de la plaque Ensuite, passer sous Cosmos Works en cliquant sur l'icône correspondant :  Il faut définir une étude (qui sera nommée plaque), en précisant analyse statique et maillage volumique. Le matériau (clic droit sur le solide) choisi sera un acier faiblement allié de coefficient de Poisson v = 0.3 et de module d'Young E = 210000 MPa. Le maillage peut être créé dès maintenant (clic droit sur maillage (mesh) puis créer ou sur l'icône correspondant, cf. figure 3). 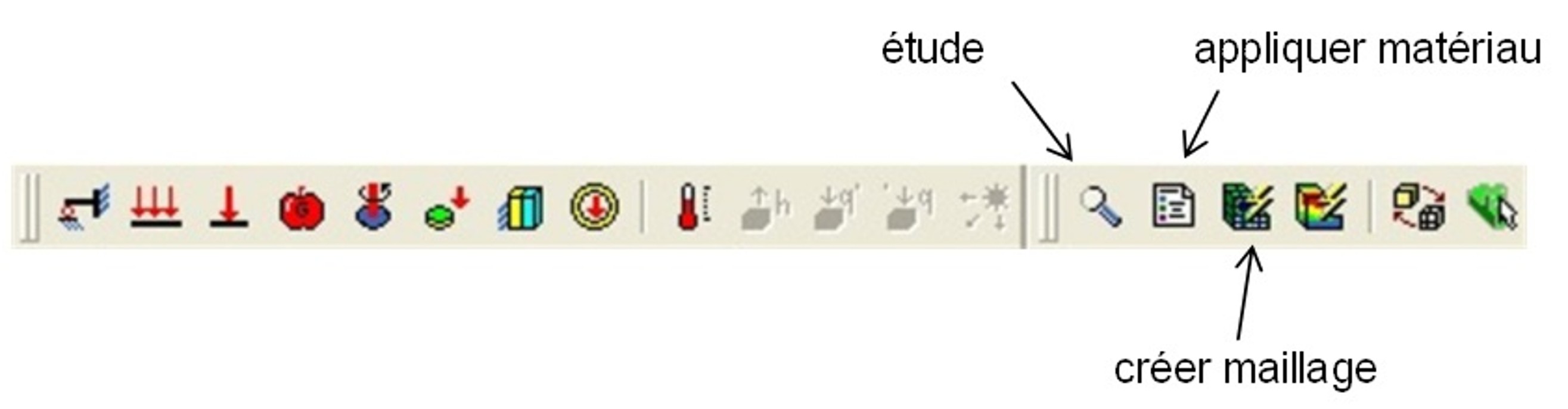 Figure 3. Présentation des barres d'outils Cosmos Le maillage (on ne peut pas changer le type d'éléments) peut être fin (fine) ou grossier (coarse) (figure 4). Il est d'ailleurs préférable, dans un premier temps, de toujours mailler grossièrement pour visualiser rapidement les zones à mailler plus finement par la suite (zones de concentration de contraintes notamment. 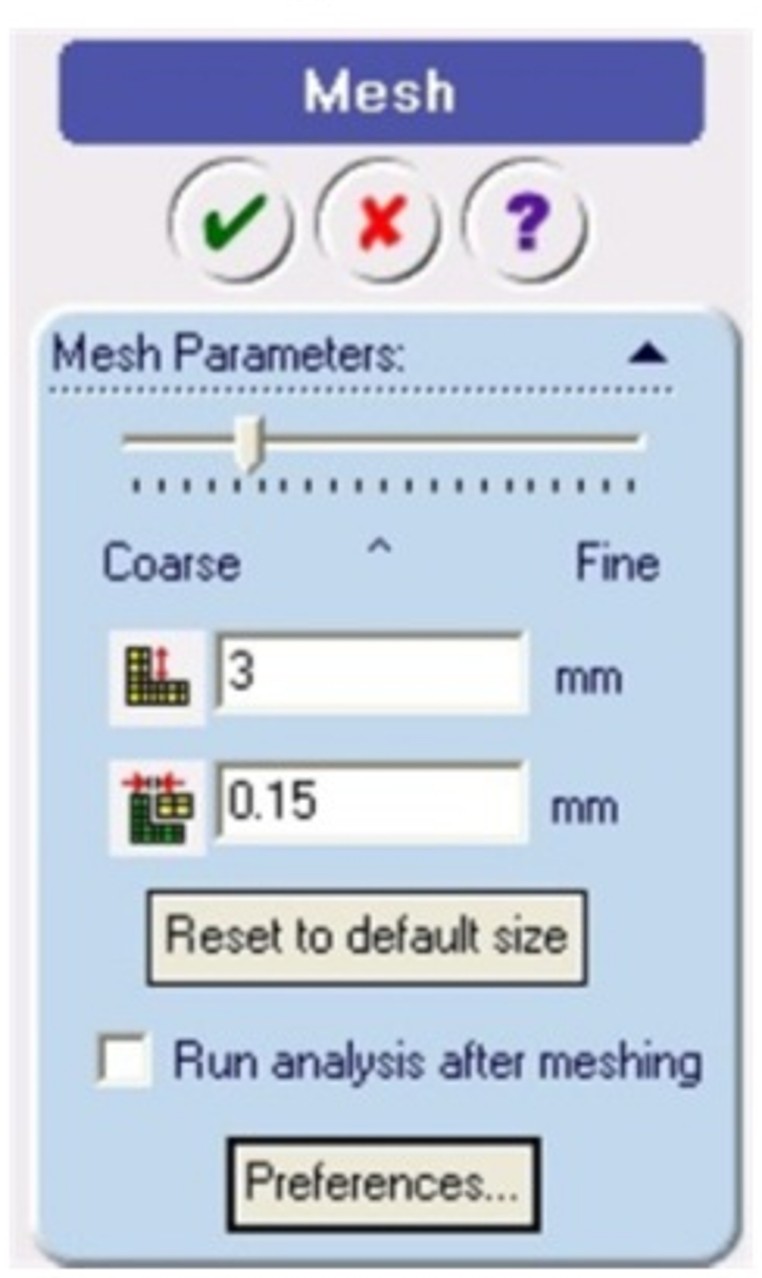 Figure 4. Paramètres du maillage Il faut ensuite définir le (ou les) chargement(s) et les conditions aux limites en déplacements du problème (clic droit sur chargement ou sur l'icône adéquat, figure 5). 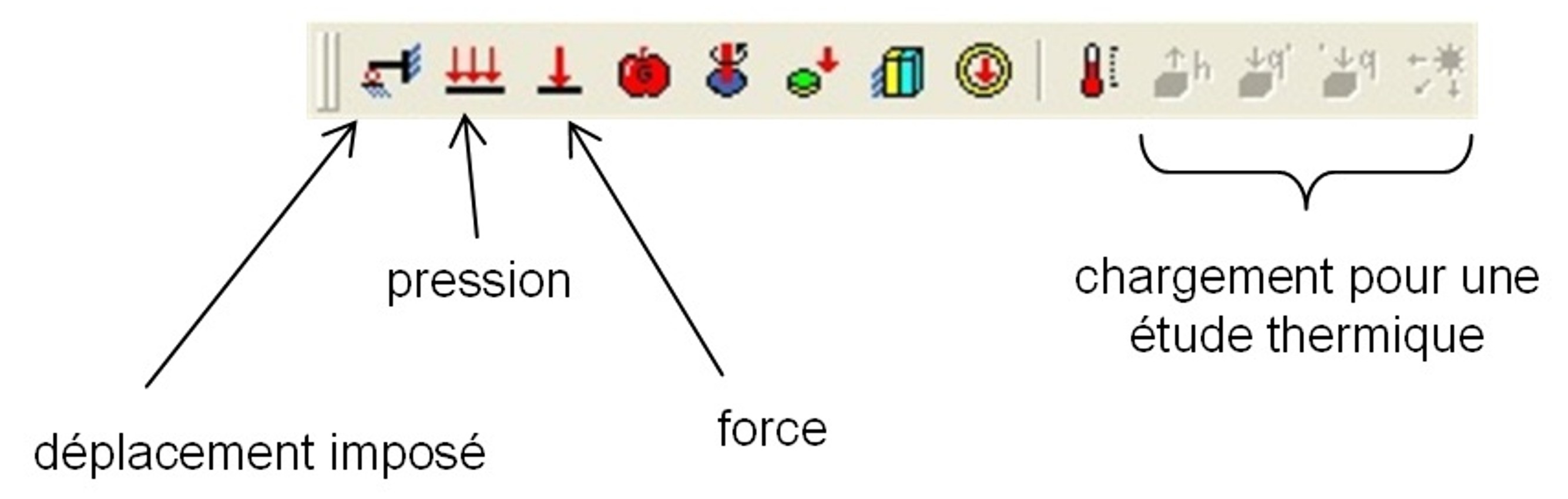 Figure 5. Icônes pour les conditions aux limites en efforts et en déplacements Remarque : pour mailler plus fin aux endroits désirés, il faut créer un contrôle (sur une ligne ou sur une surface) et y définir la taille des élements (clic droit sur maillage). On peut visualiser l'ensemble des conditions aux limites et le maillage : figure 6. 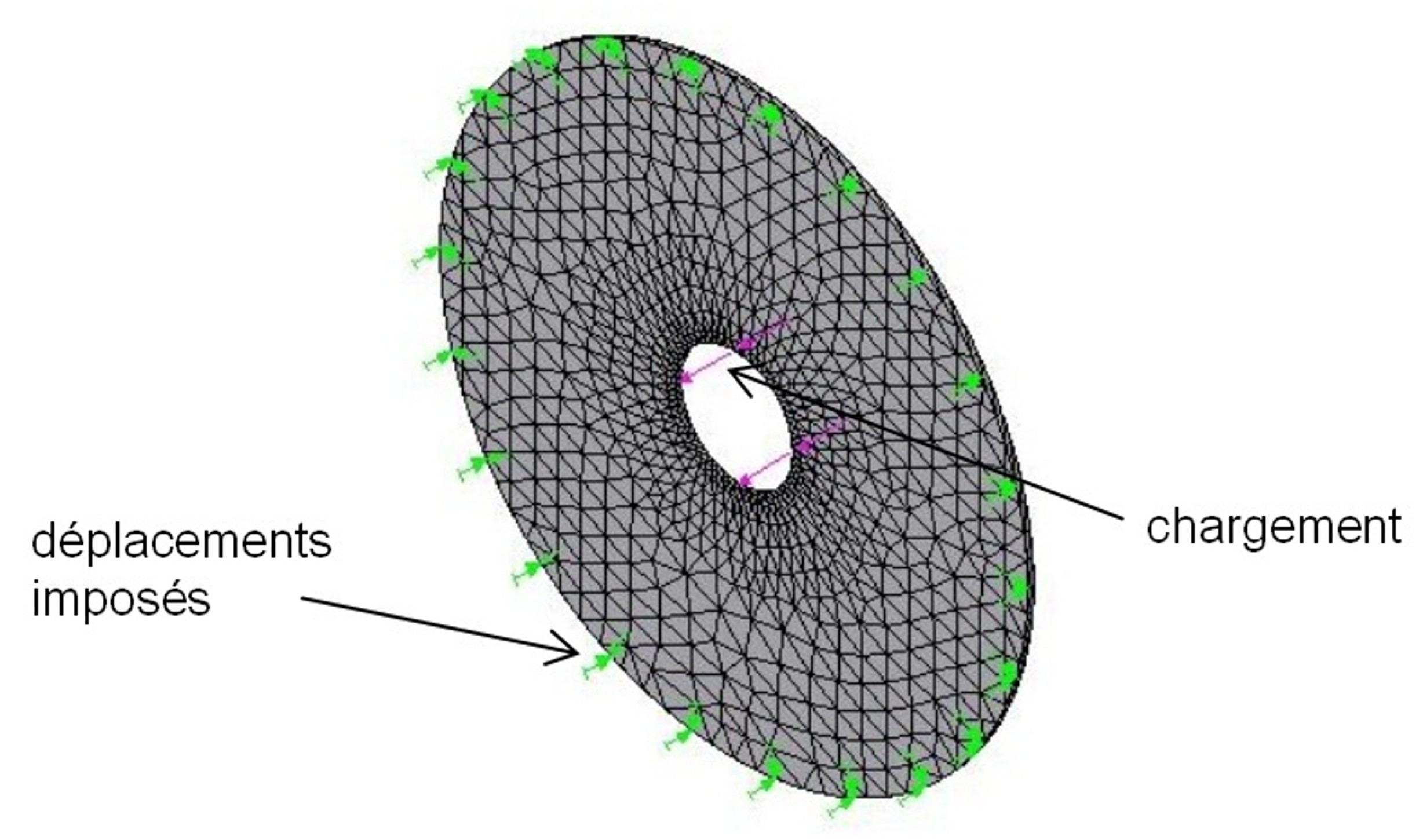 Figure 6. Exemple de maillage et conditions aux limites Le calcul peut désormais être lancé (un message d'erreurs apparaît lorsque le calcul ne peut pas se faire : problème dans les CL en déplacements, tous les ddl ne sont pas bloqués), par exemple en cliquant sur l'icône exécuter (figure 7).  Figure 7. Lancement du calcul Les résultats en contraintes et en déplacements peuvent être maintenant exploités. On peut facilement changer les unités et les composantes à visualiser (clic droit sur contraintes (stresses) et/ou déplacements). Pour connaître la valeur en un point précis, il faut visualiser les résultats sur le solide non déformé (non deformed shape) puis, à l'aide de la pipette, chercher la valeur de la contrainte (par exmple) à l'endroit désiré, voir figure 8. 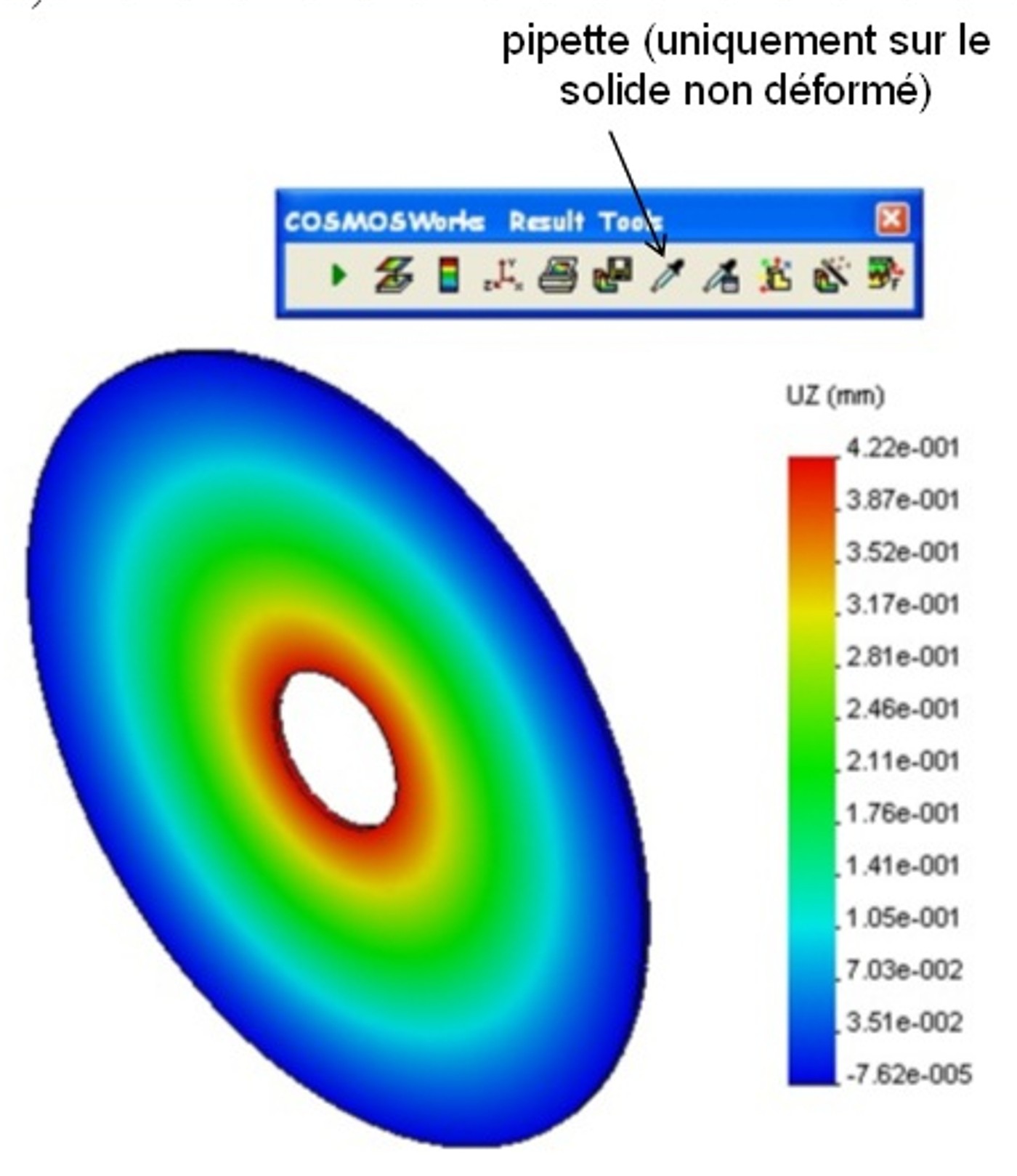 Figure 8. Exemple de résultats obtenus pour le problème Les résultats peuvent aussi être présentés sous forme animée, et également sous forme de sections, ce qui peut être, dans certains cas, très utile, voir figure 9 suivante. 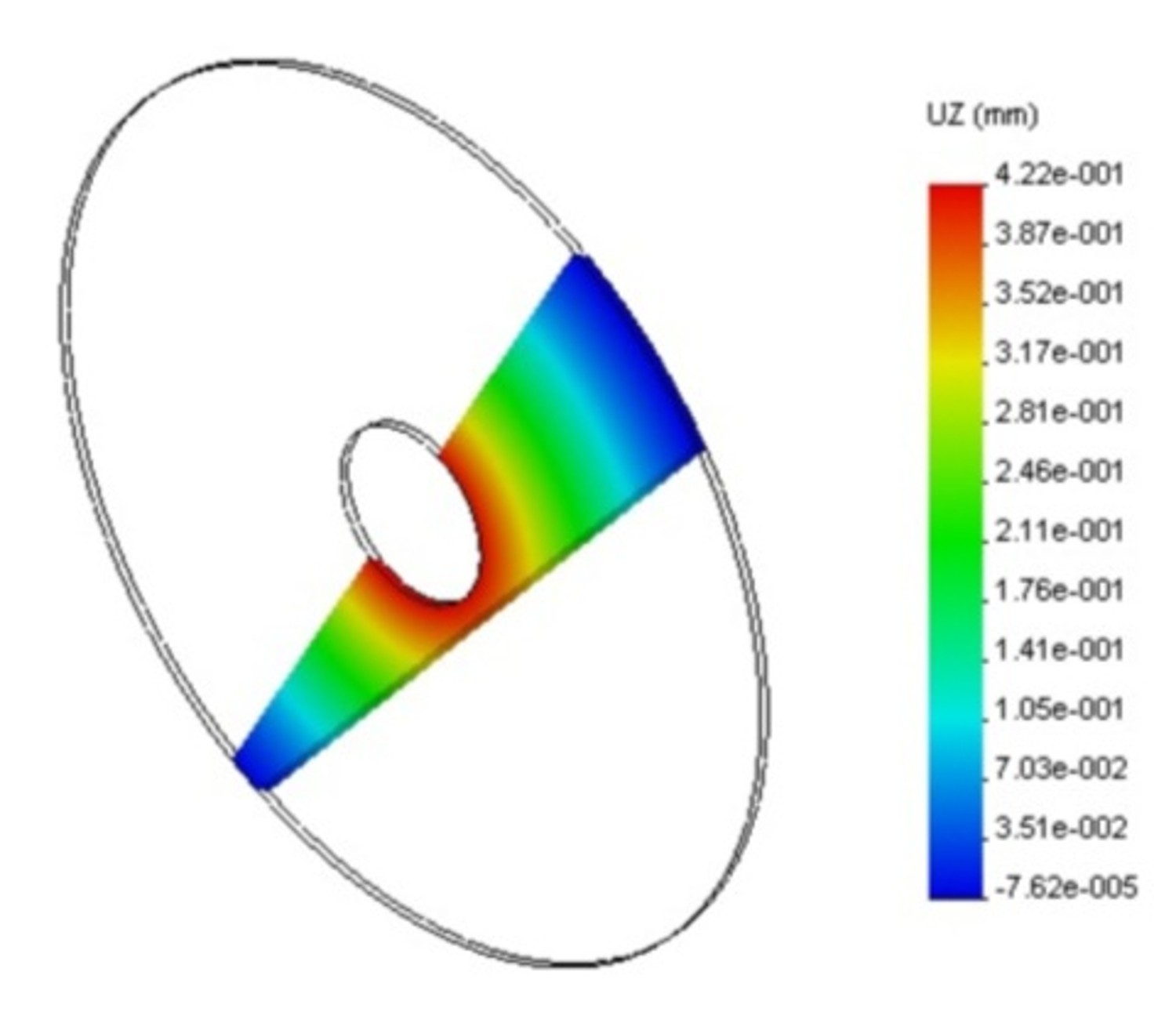 Figure 9. Exemple de résultat en utilisant des sections Exercice de vérification : le résultat de la simulation sous CosmosWorks est-il proche du modèle théorique issu de la théorie des plaques ? Exercices d'application : cliquer ici
|
