 |
|||||||
Exercices d'application 2. Contraintes résiduelles dans un tube soudé Ce problème est très simplifié, car les caractéristiques du matériau dépendent de la température (de plus, aux fortes températures, le comportement du matériau n'est plus purement élastique). Dans cette étude, l'idée est de proposer une démarche qui permette de limiter ces contraintes résiduelles, pas d'en déterminer des valeurs précises. Nous ferons donc l'hypothèse que les caractéristiques du matériau ne dépendent pas de la température. On considère un tube fendu (en fait une tôle roulée), chanfreiné, en acier faiblement allié (E = 210000 MPa, v = 0.3), dont la géométrie est présentée dans la figure 1 suivante. Sa longueur est L = 500 mm. 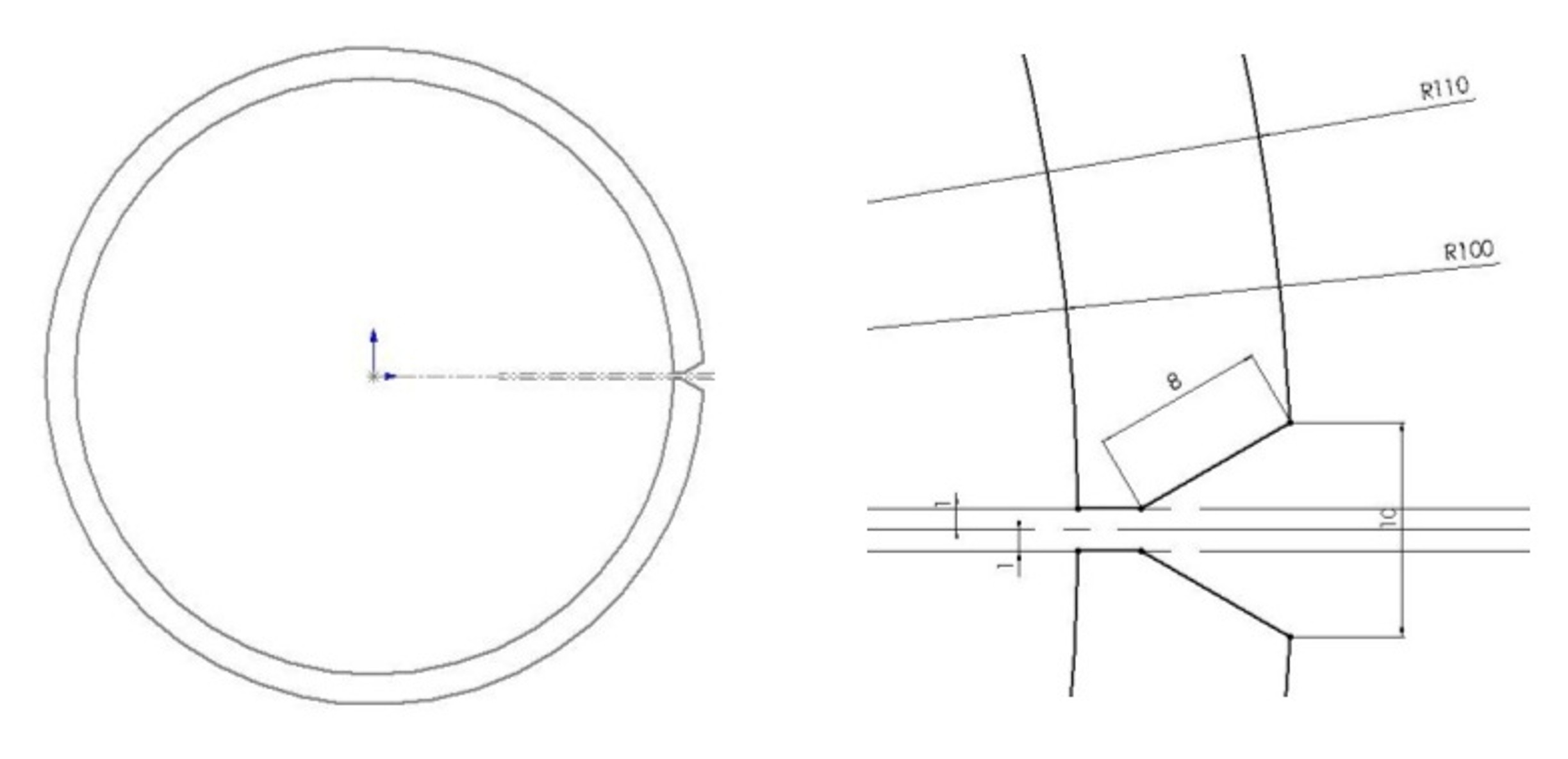 Figure 1. Géométrie du tube à souder Le cordon déposé, dont la section est assimilée à un triangle, est défini sur la figure 2. Sa longueur est l = 500 mm. 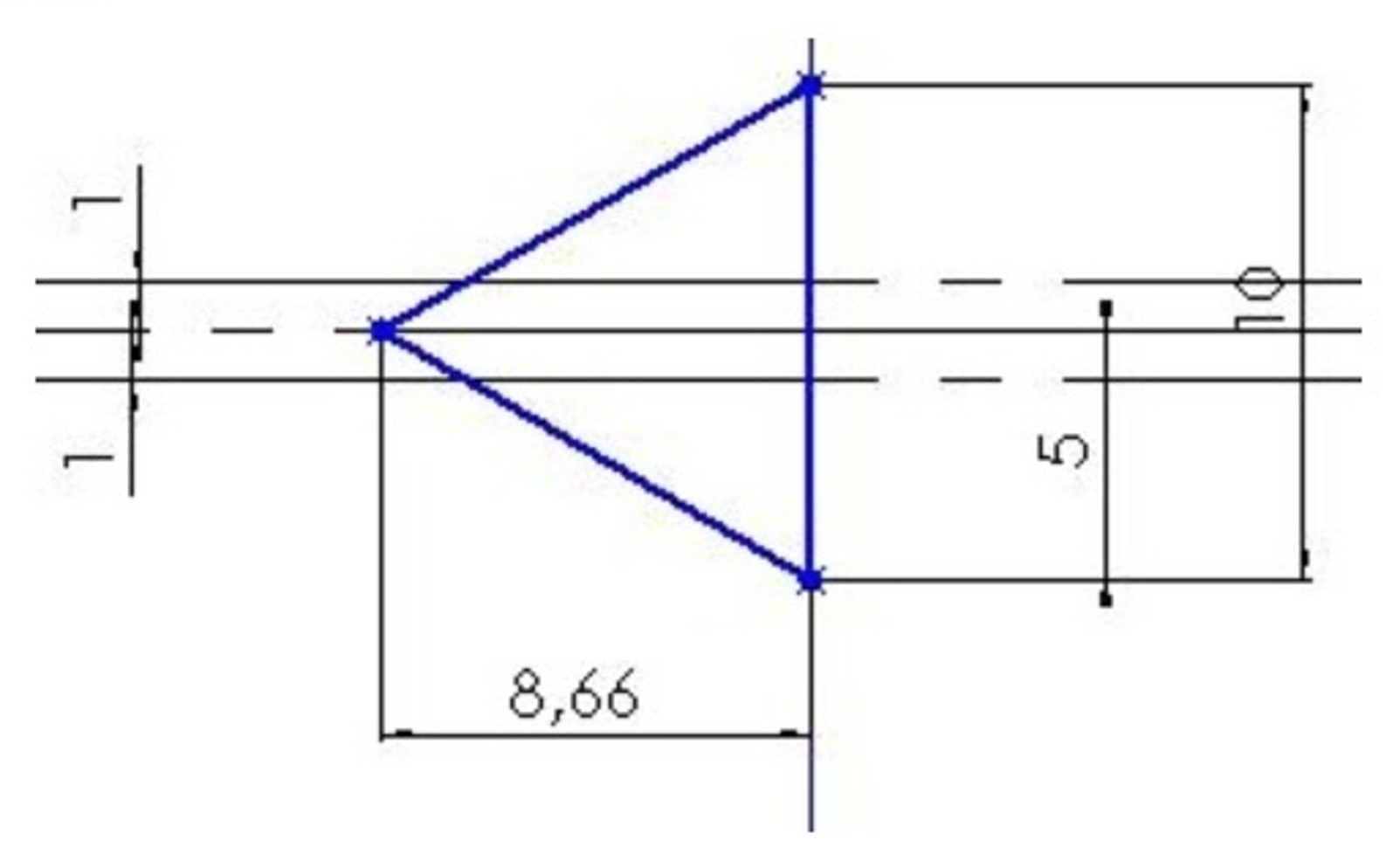 Figure 2. Géométrie du cordon Réaliser l'assemblage des deux parties avant de faire l'étude thermique sous CosmosWorks, figure 3.  Figure 3. Présentation de l'assemblage {tube + cordon} Sous CosmosWorks, faire d'abord une étude thermique : nous considérons que le cordon est déposé à Tc = 1500 K ; imposer un temps de calcul pour permettre le refroidissement de l'ensemble ainsi qu'un incrément (étude en régime transitoire). On considère, ce qui n'est pas le cas en réalité, que le tube reste à température ambiante (Tamb = 300 K). Faire ensuite une étude statique, et dans propriétés, inclure les effets thermiques et choisir le pas de calcul. Choisir un chargement et des conditions aux limites compatibles avec le problème ; on fera l'hypothèse que la dilatation du tube est bloquée. Déterminer les contraintes résiduelles de Von Mises après refroidissement. Proposer une méthode technologique pour diminuer ces contraintes.
|